Брянский городской лицей №1 имени А. С. Пушкина

Проект 8 информационно-математического класса "Теорема Пифагора и способы её доказательства"  

О проекте

О Пифагоре

История доказательства теоремы

Способы доказательства теоремы

Это полезно знать

   Участники проекта:

   Цели и задачи проекта:

  О теореме Пифагора написано огромное количество научной литературы. В ней присутствуют, в основном, современные доказательства, написанные математическим языком, но в большинстве случаев они мало понятны человеку с небольшим багажом математических знаний, поэтому мы хотели с помощью своей работы:

• Доступнее преподать материал учебника, используя такие средства, как различную дополнительную литературу, сайты Интернета.


• Сделать электронную презентацию и сайт.


• Показать значение теоремы Пифагора в развитии науки и техники многих стран и народов мира.


• В наиболее простой и интересной форме преподать содержание теоремы.

   Значение теоремы

Теорема Пифагора – это одна из самых важных теорем геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Одна из теорем позволяет убедиться в том, что если из точки вне прямой проведены к ней перпендикуляр и наклонные, то:

Теорема Пифагора была первым утверждением, связавшим длины сторон треугольников. Потом узнали, как находить длины сторон и углы остроугольных и тупоугольных треугольников. Возникла целая наука тригонометрия («тригон» - по-гречески означает «треугольник»).

Эта наука нашла применение в землемерии.

Но еще раньше с ее помощью научились измерять воображаемые треугольники на небе, вершинами которых были звезды. Сейчас тригонометрию применяют даже для измерения расстояний между космическими кораблями.

Теорема Пифагора позволяет по любым двум сторонам прямоугольного треугольника найти его третью сторону. Решая эту задачу, нам приходится по известному квадрату положительного числа находить само это число.

Благодаря тому, что теорема Пифагора позволяет находить длину отрезка (гипотенузы), не измеряя его непосредственно, она как бы открывает путь с прямой на плоскость, с плоскости в трехмерное пространство и дальше – в многомерные пространства. Этим определяется ее исключительная важность для геометрии и математики в целом.
  Применение теоремы Пифагора. Презентация.

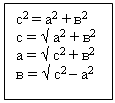
   Введение

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» - квадрате на гипотенузе, равновеликом двум квадратам на катетах.

Причина такой популярности теоремы Пифагора триедина: это простота – красота – значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал придает ей особую притягательную силу, делает ее красивой.

Кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций.

В современных учебниках теорема сформулирована так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»

Во времена Пифагора она звучала так: «Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах» или «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».

   Оргмоменты: