Брянский городской лицей №1 имени А. С. Пушкина
Проект 8 информационно-математического класса "Теорема Пифагора и способы её доказательства"
О проекте
О Пифагоре
История доказательства теоремы
Способы доказательства теоремы
Это полезно знать


Статую красит вид, а человека — его деяния.
За легендой – истина (История открытия теоремы)
Открытие теоремы Пифагора окружено ореолом красивых легенд. Прокл, комментируя последнее предложение I книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого принес в жертву быка». Легенда эта прочно срослась с теоремой Пифагора и через 2000 лет продолжала вызывать горячие отклики.
Так, оптимист Михайло Ломоносов писал:
«Пифагор за изобретение одного геометрического правила Зевесу принес на жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось».
А вот ироничный Генрих Гейне видел развитие той же ситуации несколько иначе:
«Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принес в жертву бессмертным богам».
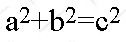
Применение теоремы
Еще в древности возникла необходимость вычислять стороны прямоугольных треугольников по двум известным сторонам.
1) Построение прямых углов египтянами.2)Нахождение высоты объекта и определение расстояния до недоступного предмета.
Подобные задачи решаются и в нашей повседневной жизни: в строительстве и машиностроении при проектировании любых строительных объектов.
История открытия теоремы
Обычно открытие теоремы Пифагора приписывают древнегреческому философу и математику Пифагору (6 в. до н.э.). Но изучение вавилонских клинописных таблиц и древнекитайских рукописей (копий еще более древних манускриптов) показало, что это утверждение было известно задолго до Пифагора, возможно, за тысячелетия до него. Заслуга Пифагора в том, что он открыл доказательство этой теоремы.
Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4».
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Также теорема Пифагора была обнаружена и в древнекитайском трактате «Чжоу – би суань цзинь» («Математический трактат о гномоне»), время создания которого точно не известно, но где утверждается, что в 15 в. до н. э. – китайцы знали свойства египетского треугольника, а в 16 в. до н. э. – и общий вид теоремы.
Кантор (крупнейший немецкий историк математики) считает, что равенство 32 + 42 = 52 было известно уже египтянам еще около 2300 г. до н.э. во времена царя Аменемхета первого (согласно папирусу 6619 Берлинского музея).
По мнению Кантора, гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 м от одного конца и 4 м от другого. Прямой угол окажется заключен между сторонами в 3 и 4 м. Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, т.е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой – на критическом изучении греческих источников, Ван-дер-Вардер (голландский математик) сделал следующий вывод:
«Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематическое обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку».
Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н.э., также о ней было известно и в древнеиндийском геометрическо-теологическом трактале 7-5 вв. до н. э. «Сульва сутра» («Правила веревки»).
Но не смотря на все эти доказательства, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадётся. То же относится и к легенде о заклинании быков Пифагора. Да и вряд ли нужно препаривать историко-математическим скальпелем красивые древние предания.
